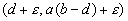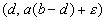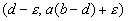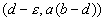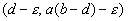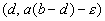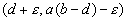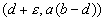3. Oplosmethode.
3.1. Numerieke Oplosmethoden
3.1.1. Waarom numeriek oplossingen bepalen?.
Dit is een goede vraag waarop vrij kort geantwoord kan worden.
We werken in dit model met een stelsel differentiaal vergelijkingen. We zouden natuurlijk kunnen proberen om dit analytisch op te lossen,
maar omdat het vaak niet mogelijk is om een dv van de vorm y'=F(x,y) expliciet uit te rekenen, is een numerieke benadering veel beter op z'n plaats.
Daarbij zijn deze vaak ook erg geschikt om in een computer te stoppen, zodat die een heleboel werk uit handen kan nemen.
3.1.2. De beschikbare (numerieke)oplosmethoden.
Uiteraard zijn er meerdere numerieke oplosmethoden te bedenken die we zouden kunnen toepassen op het stelsel differentiaal vergelijkingen
(zeker omdat ze lineair zijn, is er een keur aan methoden). We kiezen voor de Euler-Forward methode, die we nu kort zullen bespreken.
3.2 De Euler-Forward methode.
3.2.1. De werking van de Euler-Forward methode.
Stel we hebben een dv van de vorm y'=F(x,y) met een begin voorwaarde =y0.gif) .
We noemen
.
We noemen  met h erg klein. Verder noemen we
met h erg klein. Verder noemen we .gif) .
Dan kunnen we de
.
Dan kunnen we de 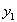 schrijven als een Taylor reeks:
schrijven als een Taylor reeks: 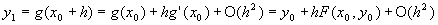 .
.
We benaderen 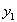 met
met 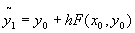 . Als nieuwe beginvoorwaarde
nemen we nu
. Als nieuwe beginvoorwaarde
nemen we nu .gif) en kunnen we op dezelfde manier
en kunnen we op dezelfde manier 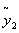 berekenen
en daarmee hebben we een benadering voor
berekenen
en daarmee hebben we een benadering voor .gif) , met
, met  .
.
Met dit proces kunnen we door blijven gaan en kunnen we de functie g benaderen (en teken), zodat we een goed beeld krijgen van de 'echte' oplossing.
3.2.2 De foutschatting in de Euler-Forward Methode.
Omdat we als benadering voor 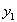 de uitdrukking
de uitdrukking 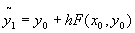 nemen, hebben we per stap een afbreekfout
van
nemen, hebben we per stap een afbreekfout
van 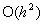 . Als we dan de nauwkeurigheid berekenen van de benadering na een interval met lengte L=nh,
dan worden al die afbreekfoutjes bij elkaar opgeteld, doordat je met de benadering doorrekent.
. Als we dan de nauwkeurigheid berekenen van de benadering na een interval met lengte L=nh,
dan worden al die afbreekfoutjes bij elkaar opgeteld, doordat je met de benadering doorrekent.
Echter, men kan aantonen dat de fout na n stappen van grootte h van orde h is (O(h)).
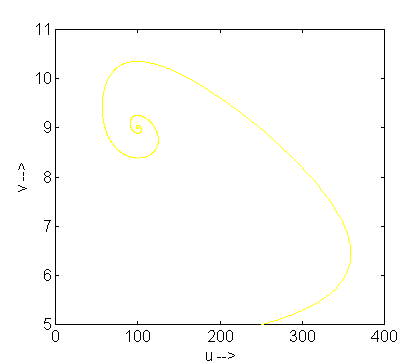
Fig. 3.1: Een benadering m.b.v. Euler-Forward van u(t) en v(t) uitgezet tegen elkaar.
3.3. Onderzoek naar stationaire punten en het richtingsveld.
3.3.1. De stationaire punten.
Zoals bekend is, komen stationaire punten alleen voor op de plekken waar aan de eisen 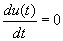 en
en 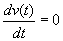 voldaan is.
Als we dit invullen in het stelsel differentiaal vergelijkingen, volgt na een redelijk simpele analyse dat er slechts drie stationaire punten zijn,
te weten: (0,0) ; (b,0) ; (d,a(b-d)).
voldaan is.
Als we dit invullen in het stelsel differentiaal vergelijkingen, volgt na een redelijk simpele analyse dat er slechts drie stationaire punten zijn,
te weten: (0,0) ; (b,0) ; (d,a(b-d)).
Het eerste punt (0,0) is natuurlijk triviaal. Als er geen konijnen en ook geen wolven zijn, blijft de situatie natuurlijk stabiel.
Het tweede punt (b,0) is ook triviaal. Er is immers een maximum aantal konijnen (b) ingevoerd. In het punt (b,0), zijn er geen wolven en
een maximum aantal konijnen. Wegens de beperking opgelegd in het model, is dit een stabiel evenwicht.
Het laatste punt (d,a(b-d)) is een stuk interessanter. Dit zou namelijk wel eens het punt kunnen zijn waarin een (stabiel)evenwicht optreedt.
Hiervoor moeten we naar het richtingsveld kijken.
3.3.2. het richtingsveld.
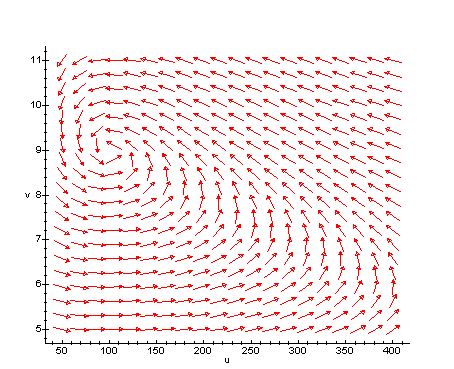
Om het richtingsveld te kunnen bepalen, hoeven we eigenlijk maar naar negen punten te kijken, waarvan er één het stationaire punt (d,a(b-d)) is.
In deze tabel geldt: epsilon>0.
|
Punt
|
du/dt
|
dv/dt
|
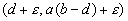
|
negatief
|
positief
|
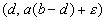
|
negatief
|
0
|
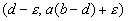
|
positief
|
positief als d<b
|
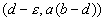
|
positief
|
negatief als d<b
|
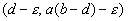
|
positief
|
negatief als d<b
|
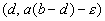
|
positief
|
0
|
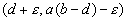
|
positief
|
positief als d<b
|
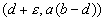
|
negatief
|
positief als d<b
|
Omdat het maximum aantal konijnen (b) altijd groter is dan het eindaantal konijnen (d), levert deze tabel het volgende plaatje op:
Fig 3.2: Het richtingsveld van de oplossing.



=y0.gif) .
We noemen
.
We noemen  met h erg klein. Verder noemen we
met h erg klein. Verder noemen we .gif) .
Dan kunnen we de
.
Dan kunnen we de 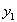 schrijven als een Taylor reeks:
schrijven als een Taylor reeks: 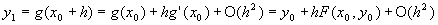 .
.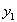 met
met 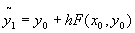 . Als nieuwe beginvoorwaarde
nemen we nu
. Als nieuwe beginvoorwaarde
nemen we nu .gif) en kunnen we op dezelfde manier
en kunnen we op dezelfde manier 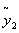 berekenen
en daarmee hebben we een benadering voor
berekenen
en daarmee hebben we een benadering voor .gif) , met
, met  .
.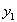 de uitdrukking
de uitdrukking 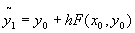 nemen, hebben we per stap een afbreekfout
van
nemen, hebben we per stap een afbreekfout
van 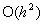 . Als we dan de nauwkeurigheid berekenen van de benadering na een interval met lengte L=nh,
dan worden al die afbreekfoutjes bij elkaar opgeteld, doordat je met de benadering doorrekent.
. Als we dan de nauwkeurigheid berekenen van de benadering na een interval met lengte L=nh,
dan worden al die afbreekfoutjes bij elkaar opgeteld, doordat je met de benadering doorrekent.
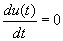 en
en 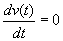 voldaan is.
Als we dit invullen in het stelsel differentiaal vergelijkingen, volgt na een redelijk simpele analyse dat er slechts drie stationaire punten zijn,
te weten: (0,0) ; (b,0) ; (d,a(b-d)).
voldaan is.
Als we dit invullen in het stelsel differentiaal vergelijkingen, volgt na een redelijk simpele analyse dat er slechts drie stationaire punten zijn,
te weten: (0,0) ; (b,0) ; (d,a(b-d)).