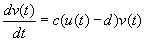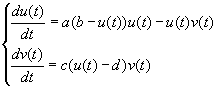2. Probleemstelling


2.1. De Vraagstelling

Het probleem is als volgt:
Stel we hebben een gebied met konijnen en wolven. Dan zijn er een aantal vragen waar men naar kan kijken, zoals: Wat gebeurt er wanneer, oftewel, welke mogelijkheden zijn er? Sterft één van de soorten misschien uit? Wat is de afhankelijkheid van de twee soorten? Zijn er meer diersoorten die invloed hebben? Zou er een stabiele situatie kunnen optreden?
Dit zijn allemaal vragen die (bijna) vanzelfsprekend om de hoek komen kijken bij twee (of meer) populaties van dieren. Om dit (wiskundig) goed te kunnen onderzoeken, is een model nodig.


2.2. Het Model

2.2.1. De sociale achtergrond van het gebruikte model.

Om een (goed) model te kunnen maken, waar ook nog wat aan te rekenen is, moet je wel een aantal beperkingen (vereenvoudigingen) hanteren. Dit doen we dus ook.
Ten eerste gaan we er vanuit dat het geheel zich afspeelt in een beperkt, vast en afgesloten gebied. Dit impliceert echter ook dat er geen dieren in of uit het gebied gaan, geen migratie dus.
Verder nemen we aan dat de wolven (roofdieren) slechts leven van de konijnen (prooidieren). Dit geeft een aantal zekerheden, bijvoorbeeld: stel dat het aantal konijnen daalt, dan zal dit direct te merken zijn in het aantal wolven. Sterker: als de konijnen uitsterven, zullen de wolven dit ook doen.
De wolven hebben nu te eten, maar waar leven de konijnen van? Dit is niet relevant voor mijn probleem. We gaan er vanuit dat er genoeg voedsel is voor alle konijnen hoeveel dit er ook zijn.
Dit brengt ons tot een andere aanname: zoals alle dieren planten konijnen zich voort (en hoe!). Maar omdat we een bepaald, afgesloten gebied bekijken, kunnen er maar een maximaal aantal konijnen in dat gebied leven. Op een gegeven moment is er gewoon geen eten meer voor al die beesten. Vandaar dat we een maximum stellen aan het aantal konijnen. (of dit ook een maximum van het aantal wolven bepaald is nog niet bekend).

2.2.2. Wiskundig model

Natuurlijk hoort bij een "maatschappelijk" model ook een wiskundig model (althans, in de wiskunde). Je moet er tenslotte aan kunnen rekenen. We zullen nu een en ander nader uitwerken m.b.t. het gebruikte wiskundige model.
We moeten dus proberen twee functies te bedenken die een goede afspiegeling zijn van de werkelijkheid. Laten we eerst beginnen met de (standaard) functies zelf. We noemen deze u(t) en v(t), resp. van de prooidieren en de roofdieren. (omdat we naar de veranderingen van de aantallen prooi- en roofdieren willen kijken, nemen we u en v afhankelijk van de tijd.
De toename van het aantal dieren zal afhangen van het aantal dieren. Dan komen we dus uit op twee differentiaal vergelijkingen: (1)      
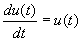
(2)      
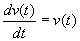
In deze vorm is het echter zo, dat de toename per tijdseenheid gelijk is aan het aantal dieren. Dit is natuurlijk onzin en dus zullen we er een extra variabele in moeten stoppen: de zogenoemde "groeifactor". Dit levert ons het volgende:
(3)      
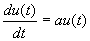
(4)      
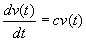
Nu het echter ook zo, dat we hebben gesteld dat er een maximum aan het aantal konijnen is. Dan zullen we weer de formule moeten veranderen, en weer een extra variabele moeten invoeren, nl. het maximum (al dan niet afhankelijk van de tijd). Hieruit volgt dan de volgende formule:
(5)      
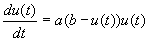
(of, als we het maximum tijdsafhankelijk willen nemen: (6)           )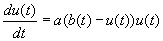
Zoiets dergelijks kunnen we ook met de vergelijking voor de wolven doen, al gebruiken we dan niet het maximum aantal konijnen, maar het aantal dat we aan het eind willen overhouden:
(7)      
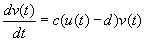
Dan is er nog een laatste stap te maken. Een deel van de konijnen wordt (hoogst waarschijnlijk) op gegeten door de wolven, dus niet alle konijnen kunnen nakomelingen krijgen. We moeten het deel dat opgegeten wordt er eerst nog van aftrekken. Dan krijgen we uiteindelijk het volgende stelsel differentiaal vergelijkingen:
(8)      
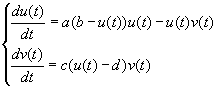
(We kunnen b natuurlijk ook hier tijdsafhankelijk nemen, maar dan wordt het geheel een stuk ingewikkelder. Dit geldt ook voor het product van u(t) en v(t) in de eerste dv van (8). Hier zou misschien nog een coëfficient voor moeten, maar ook dan wordt het een stuk ingewikkelder.)

---
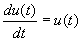
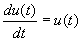
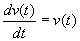
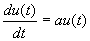
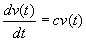
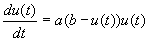
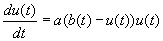