Solvers for the Maxwell equations: application the determination of the
radar signature of modern fighter aircraft
Shiraz Abdoel
Site of the project:
National Aerospace Laboratory NLR
NLR Amsterdam
Anthony Fokkerweg 2
1059 CM Amsterdam
start of the project:
March 2008
In May 2008 the
Interim Thesis has been appeared
and a
presentation has been given.
The Master project has been finished in December 2008
by the completion of the
Masters Thesis
and a final presentation has been given.
At the alumni meeting the following
poster
has been presented.
For working address etc. we refer to our
alumnipage.
Summary of the master project:
Radar cross section prediction techniques are used to
determine the radar
signature of a military platform (for example an aircraft, ship or
tank) when the radar signature can not be
determined experimentally, because the platform is not available or for reasons of time
and cost.
F16 Fighter Jet

For classic
jet aircraft the radar cross section for forward observation angles is
dominated by the
contribution of the open ended cavity formed by the jet engine air
intake and compres-
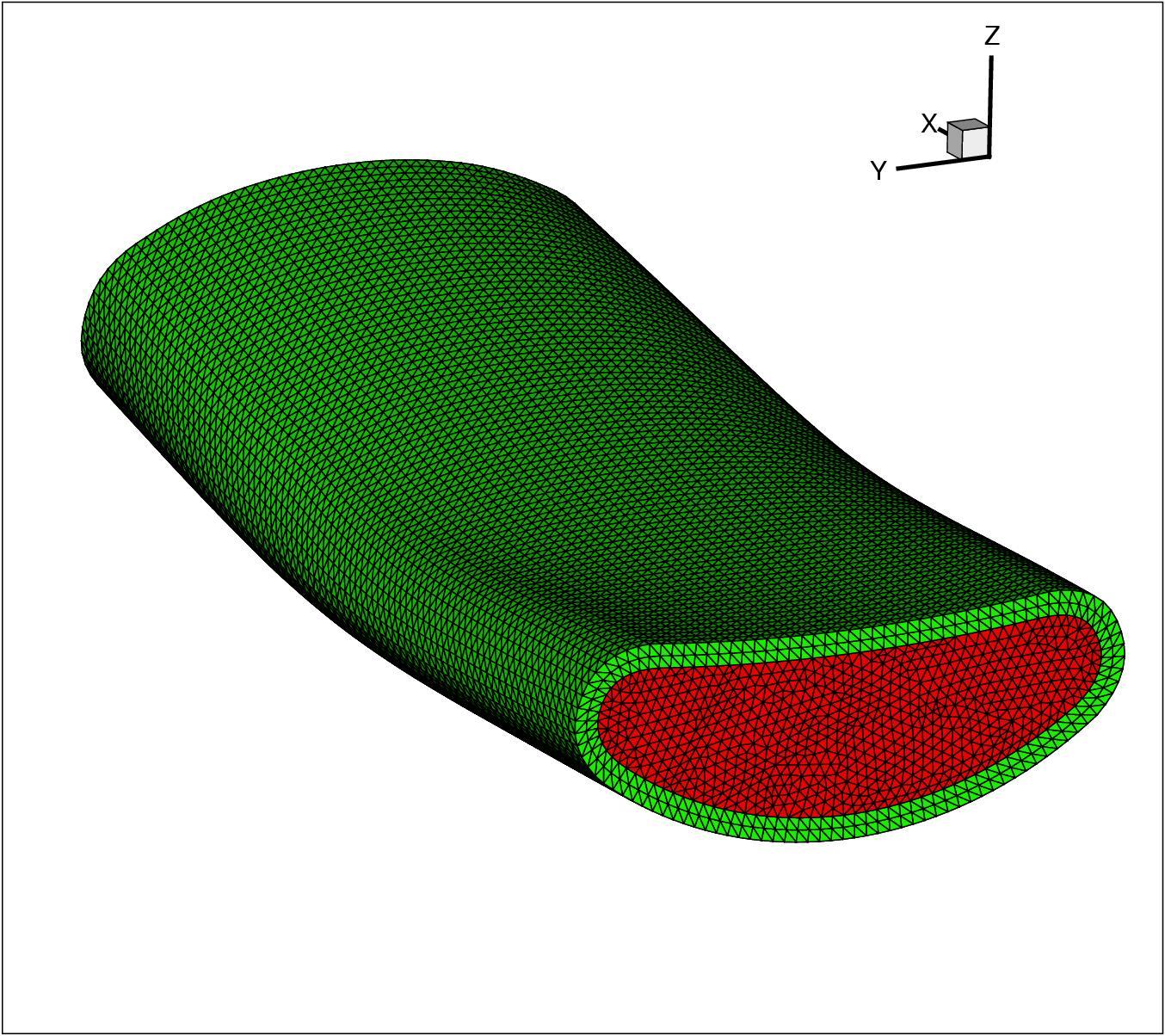
sor fan. This cavity is characterized by its large depth (L/d > 3),
curved centerline and
nonuniform cross section, for which the scattering characteristics can
not by analyzed by
approximate high frequency methods. Jin et al. have published a
numerical method based
on a higher order finite element discretisation of the Maxwell
equations, where the re-
sulting linear system is solved by means of a frontal solution method.
The method takes
full advantage of the topology of the cavity scattering problem and has
been successfully
applied for the analysis of cavities of intermediate size. In van
der Heul etal.
an adaptation of
their algorithm is discussed that can efficiently compute the electric
field scattered by very
large cavities, in particular the jet engine air intake cavity for
X-band radar frequencies (10 GHz=0.03m).
Air intake and compressor


In this master thesis project a faster and more memory efficient method
is looked after. Possibilities are faster direct solvers, parallel
computing, domain decomposition, shifted preconditioners combined with
Krylov subspace methods, etc.
Tetrahedral grid of a jet engine air intake

Contact information:
Kees
Vuik

Back to the
home page
or the
Master students page of Kees Vuik




![]()
![]()