Een onderzoek aan de Boundary Element Methode voor nauwkeurige
localisatie van hersenactiviteit ( figuren)
Raymond van Gent
Plaats van afstuderen:
MEG Centrum KNAW
Academisch Ziekenhuis Vrije Universiteit
poli receptie C
De Boelelaan 1117
1081 HV Amsterdam
start van afstuderen: september 1997
In december 1997 is de
scriptie verschenen.
De afstudeeropdracht is juni 1998 afgerond met het schrijven van het
afstudeerverslag.
Huidige adresgegevens etc. zijn te vinden op onze
alumnipagina.
Korte omschrijving van de afstudeeropdracht:
Meerkanaals MEG en EEG signalen kunnen worden gebruikt om de
onderliggende neurale activiteit te localiseren. Hiertoe wordt een
mathematisch model opgesteld dat het verband geeft tussen de electrische
bron en de gemeten signalen. Dit model beschrijft enerzijds de geometrie
van de geleider en de invloed hiervan op het elektromagnetisch veld en
anderzijds de geometrie en de tijdsafhankelijkheid van de bron. Wanneer de
geometrie van de geleider bekend is en wanneer de bron door een beperkt
aantal parameters beschreven wordt (bijvoorbeeld een stroomdipool) dan is
bronlocalisatie probleem teruggebracht tot een
parameterschattingsprobleem: bepaal die set bron parameters die de
metingen zo goed mogelijk beschrijven.
De nauwkeurigheid waarmee electrische bronnen in de hersenen
gelocaliseerd kunnen worden wordt in belangrijke mate bepaald door de
nauwkeurigheid van het gebruikte geleidingsmodel. Het eenvoudigste model
van het hoofd bestaat uit een set concentrische bolschillen, met ieder
hun eigen geleidbaarheid. Deze schillen stellen voor: de hersenen, de
cerebrospinale vloeistoflaag, de schedel en de huid. Het
bolschillenmodel
is analytisch oplosbaar en geeft een snel algoritme, maar geometrische
nauwkeurigheid is uiteraard beperkt.
Met de zogenaamde Boundary Element Methode (BEM) kan een realistisch gevormd
hoofd worden gemodelleerd dat bestaat uit homogene compartimenten van
constante geleidbaarheid. Hiertoe wordt een randintegraalvergelijking
opgesteld voor de potentiaal op de scheidingsoppervlakken. Deze
integraalvergelijking kan worden opgelost door een driehoeksbelegging te
maken van de compartimenten. Op elk van de driehoekjes wordt de
potentiaal constant verondersteld of deze kan een lineair of kwadratisch
verloop hebben. Hiermee wordt de integraalvergelijking gediscretiseerd
en gaat deze over in een systeem van lineaire vergelijkingen dat
numeriek
kan worden opgelost.
Bij het localiseren electrische bronnen uit MEG/EEG signalen wordt voor
een groot aantal combinaties van bronnen de potentiaal en het
magnetische veld uitgerekend. Daarom is het toepassen van realistische
modellen een afweging van snelheid en nauwkeurigheid. Hoe meer
driehoekjes worden meegenomen en hoe groter de orde van de interpolatie
over de driehoekjes, hoe nauwkeuriger het model, maar hoe langzamer het
algoritme. Met behulp van
simulaties willen we er achter komen waar het optimum in
de praktijk ligt.
Onderzoeksvragen
- Is het noodzakelijk om voor elk hoofd een apart driehoeksmodel af te
leiden (bijvoorbeeld van een bijbehorende MR-scan)? Of is het mogelijk om
door middel van een
beperkt aantal vervormingen van een "standaard hoofd" uit te gaan?
- Hoe fijnmazig moet de driehoeksbelegging gekozen worden om tot een
bepaalde nauwkeurigheid te komen?
- Is een locale verfijning mogelijk, cq
wenselijk?
- Heeft het zin om hogere orde interpolaties op de driehoeken te gebruiken
ten einde de nauwkeurigheid van de methode te vergroten? Of neemt
hierdoor alleen de grootte van het systeem van vergelijkingen toe?
- Kan met een grovere driehoeksbelegging worden volstaan wanneer gekromde
driehoeken worden gebruikt in plaats van de gebruikelijke platte driehoeken?
Wegen de extra kosten hier tegen op?
- Welke andere mathematische technieken kunnen worden gebruikt om de BEM
te
verbeteren (isolated problem approach, multiple deflation, Galerkin)?

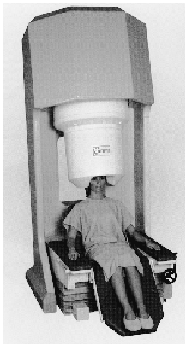
Een MEG meting

Back to
home page
or
Afstudeer pagina
of Kees Vuik
![]()

![]()
![]()

![]()