Mesh Generation in Underground Layers Near Faults ( figuren)
Abdelkader Hajjaoui

Plaats van afstuderen:
Shell Research
Volmerlaan 8
2280 AB Rijswijk
start van afstuderen: september 1997

De afstudeeropdracht is mei 1998 afgerond met het schrijven van het afstudeerverslag.

Korte omschrijving van de afstudeeropdracht:
Shell is one of the major oil companies, serving customers in most of the countries of the world. The main activities are exploring for hydrocarbons (oil and gas), production of oil and gas from the reservoirs in the earth, refining the crude oil into products and selling these.

In SIEP-EPT technical advice and research is carried out for the Shell companies involved in exploration and production of hydrocarbons for reservoirs. Within SIEP-EPT, the HM ( Hydrocarbon systems Modeling) group has the task to add value to Shell's business by providing integrated solutions to basin-scale geological problems. Hydrocarbon systems Modeling involves the physical description of a sedimentary basin in space and geological time. This means that one tries to describe how the basin was formed, and how the sediments and pore fluid, including hydrocarbons, were generated and migrated. Insight in the forming of hydrocarbons and how they moved is essential in deciding where search for hydrocarbons reservoirs.

The current areas of direct application to exploration are :

• Calculation of source rock temperature histories for use in hydrocarbon generation.
• Hydrocarbon generation.
• Migration of hydrocarbons from source rocks to reservoir rocks.
• Overpressure for safe and cost effective drilling strategies.

The HM group uses mathematical models as powerful techniques for resolving temperature problems and overpressure problems in underground layers. In general, the mathematical model of earth processes is based on the conservation of the basic properties involved e.g heat,mass and momentum. The description of all these processes result in a coupled system of partial differential equations. Such equations have only a unique solution when a series of boundary and initial conditions are imposed.

In general, the applicability of analytical methods is limited to problems with configurations of simple shape and composition. In practice, however, we are often confronted with complex geometries and with non linear terms. Due to the availability of high-speed, large-capacity digital computers, numerical techniques play an increasing important role in earth process calculations. The main advantage of these techniques is their general applicability: they are flexible with regard to shape, size and physical composition of different geometrical constituents that together form the configuration that one wants to analyze.

The numerical techniques are based on a discretization of the equations governing the relevant physical processes, as the temperature and overpressure modelling. To solve the partial differential equations, discretization techniques are used. For simple geometries one usually applies finite difference methods, but if the region becomes more complex, finite element methods are more flexible.

In sedimentary basins, faults act as both seals and conduits for fluid flow. Processes such secondary migration , temperature distribution and overpressure development depend critically on the fault pattern. In the present Shell program that is used to predict temperature and overpressures in a geological setting, a finite element mesh is used, which consists of four node quadrilaterals in two dimensions, and of eight node hexahedrons in three dimensions. The grid generator does not take into account where the faults are. As a consequence very undesirable meshes will be generated.

It is the aim of this research to adapt this finite element mesh such that acceptable meshes necessary for the computations arises. The mesh generator must satisfy certain requirements :

• Quality to ensure reasonable element shapes and to control element size.
• Efficiency with regard to computational time and memory. Further the present mesh must be kept as much as possible for these parts at a certain distance of the fault.
• A correct representation of discontinuities in the underground layer see Figure 1.
• Tetrahedra elements must be used.

An additional feature of this grid generator is that it should be able to handle regions which change position with geological time.



One horizon and a number of faults

A brief description of how the unstructured grid generation in the neighborhood of faults will be developed is as follows:

1. Investigate the supplied grids.
   
   
2. Provide mapping : A piecewise linear mapping is used to map the fault plane onto the computational space, where the structure of the intersection between horizon and fault node is retained see Figure 2.
   
   
   
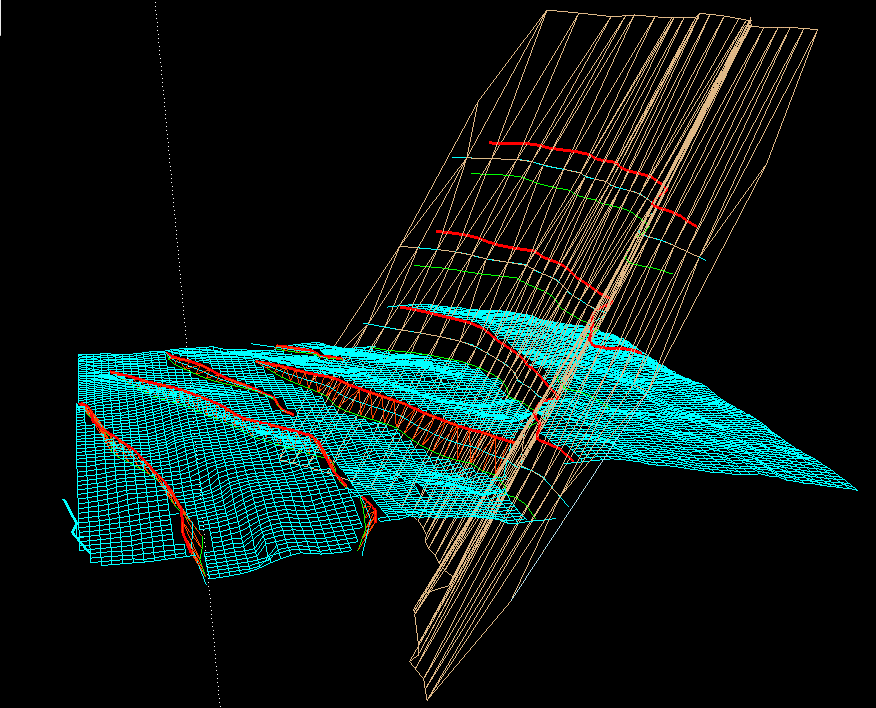
   One horizon and the fault plane
   
   
3. Creation triangulation process : The triangulation of the fault plane will be applied in the computational space in such way that :
   
   
   • The intersection line of the horizon grids and the fault plane must be part of the grid after creation of the unstructured triangular elements see Figure 3. And some node points which represent the intersection between some grid plane and the fault plane must be part of the grid.
     
     
     
     Two horizons and the fault plane
     
     
4. The inverse mapping : The inverse of the linear mapping is used to construct the fault plane in three dimensions from the two dimensional surface in the computational space.
   
   
5. Create tetrahedral mesh : The triangulated fault plane in three dimensions is extended to a domain with tetrahedral elements in such a way that :
   
   
   • The fault plane must be represented by one surface grid. The fault plane must be present in the three dimensional mesh.
     
     
6. Connect hexahedron elements with tetrahedron elements : The unstructured tetrahedral meshes in three dimensions will be connected to the hexahedron tetrahedral mesh at a certain distance from the faults.
   
   

---

Back to home page or Afstudeer pagina of Kees Vuik