Stability for boundary layers formed by salt water flow in
a porous medium
( figuren)
Gert-Jan Pieters
Plaats van afstuderen:
TU Delft en CWI
Start van afstuderen: februari 2000
De afstudeeropdracht is in september 2000 afgerond met het schrijven van
het
afstudeerverslag.
Huidige adresgegevens etc. zijn te vinden op onze
alumnipagina.
Korte omschrijving van de afstudeeropdracht:
Upflowing salty groundwater, evaporating completely at the ground
surface,
leads to the buildup of a saline boundary layer, usually with solid
salt on the
surface. The diffusion layer below the surface, if stable, may grow to
a finite
thickness at equilibrium between the upflowing salt and downward
diffusion.
Because of the different densities of the fluids (low fresh water
density in
the deeper underground and high salt water density at the boundary
layer),
gravitation plays a crucial role in the process and therefore it cannot
be
neglected. For the instable case, at a critical Rayleigh number,
perturbation
of the system results in fresh-salt fingering of the boundary layer.
The
process described above is mathematically modelled using a scaled,
coupled and
non-linear set of partial differential equations for the incompressible
fluid
including a convection-diffusion equation and Darcy's law. In this
report we
first give an overview of semi-analytical methods to analyse the
stability of
the boundary layer. Subsequently we focus on Finite Element (FEM)
solutions of the governing equations to validate numerically the
semi-analytical stability bounds. Furthermore, we analyse stability
with
respect to several kinds of perturbations.
References
C.J. van Duijn, R.A. Wooding and A. van der Ploeg.
Stability criteria
for the boundary layer formed by throughflow at a horizontal surface
of a porous medium.> submitted to Water Resources, 1999.
Guus Segal. SEPRAN manuals. Leidschendam, 1984.
Hieronder staan een aantal figuren uit het afstudeerverslag.
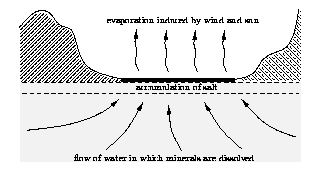
Transport of water to the surface, accumulation of salts and
evaporation of water at the surface.
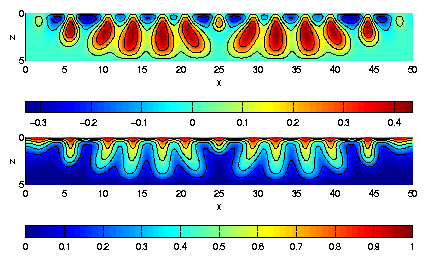
Saturation profiles
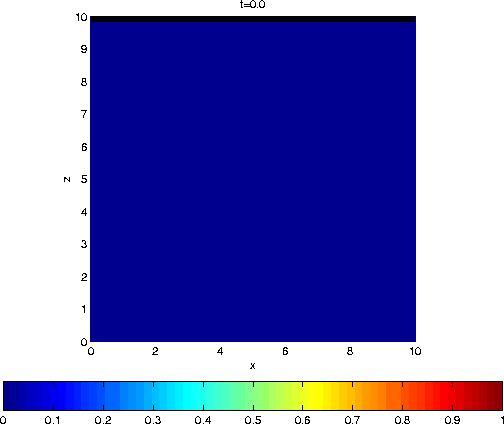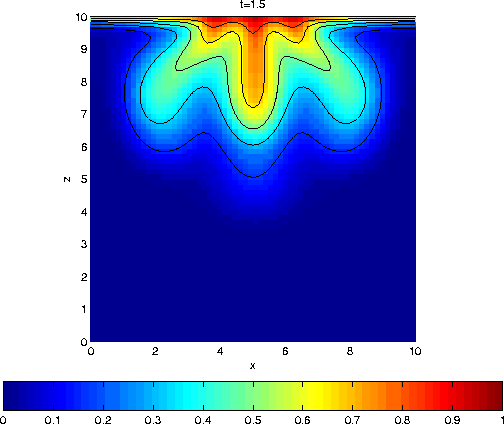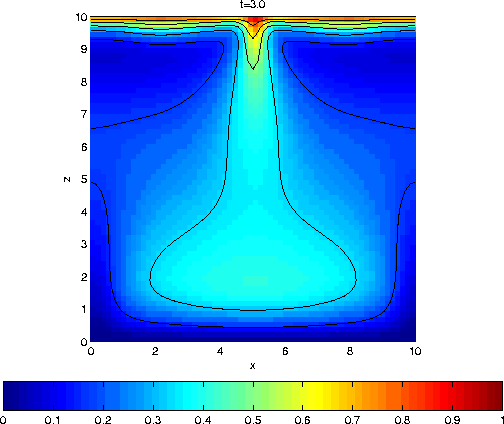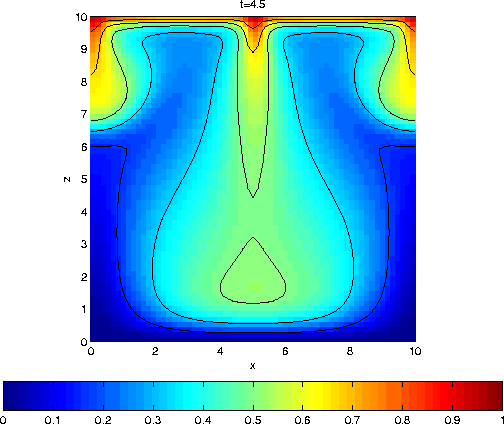
Unstable situation (Ra = 75).
The diffusion layer at the subsurface is perturbed with a
small
perturbation (5E-4). Now we have a full deformation of
the layer
and fresh-salt fingering occur.

Unstable situation (Ra = 50).
The diffusion layer at the subsurface is perturbed with a
sinusoidal
perturbation (alpha = 0.5) with small amplitude (5E-4).
Again we
have a full deformation of the layer and fresh-salt
fingering occur.

Contact informatie:
Kees
Vuik

Terug naar de
home page
of de
afstudeerpagina van Kees Vuik
Laatst aangepast op 14-11-2000 door Kees Vuik




![]()
![]()