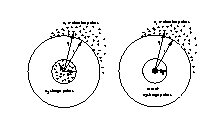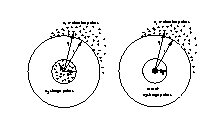Het onderzoeken van de capaciteit extractie
( figuren)
Willemijn van Til
Plaats van afstuderen:
Delft University of Technology
Faculteit electrotechniek, vakgroep Circuits And
Systems (CAS)
Mekelweg 4
2628 CD Delft
start van afstuderen: februari 1997
De afstudeeropdracht is in 1998 afgerond met het schrijven van het
afstudeerverslag en een
testverslag.
Huidige adresgegevens etc. zijn te vinden op onze
alumnipagina.
Korte omschrijving van de afstudeeropdracht:
In de electrotechniek is het gedrag van een chip belangrijk. De chips
worden steeds kleiner en de parisitaire elementen spelen een steeds
groter
wordende rol bij het bepalen van het gedrag van de chip. De parisitaire
elementen zijn de weerstand, de inductie en de capaciteit.
Mijn afstudeeropdracht richt zich op het parisitaire element capaciteit.
Om de capaciteiten te kunnen extraheren wordt er gebruik gemaakt van de
Boundary Element Method. De meeste tijd van de BEM zit in het inverteren
van een volle matrix. Nu zijn niet alle gegevens in de matrix relevant
voor het gedrag. Deze gegevens kunnen op nul worden gesteld, omdat de
afstand tussen de elementen te groot is, is de capaciteit
verwaarloosbaar.
Het SCHUR algoritme is een methode die niet de hele matrix berekend en
inverteerd. Deze methode maakt gebruik van een maximum afstand waarin de
capaciteiten invloed hebben op elkaar.
Een andere methode schat met behulp van multipole expansie de
capaciteiten. Hiervoor wordt het gebied gediscretiseerd op een speciale
manier. Door de discretisatie kan gebruik worden gemaakt van
schuifmatrices en conversiematrices. Deze matrices hoeven maar een keer
voor het hele proces berekend te worden.
De bedoeling van het onderzoek is een combinatie van de beste
eigenschappen van beide methoden. De FastCap methode is snel maar
gebruikt veel geheugen. De Schur methode gebruikt weinig geheugen maar
kost meer tijd. De nieuwe methode moet dus even snel of sneller zijn dan
FastCap en minder geheugen of evenveel geheugen gebruiken als Schur.
Hieronder staan een aantal figuren uit het afstudeerverslag.

Detail of a 3D model for a static RAM array
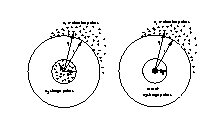
The evaluation points and the point charges for a multipole
expansion
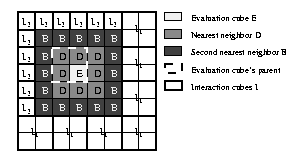
A two-dimensional representation of the division
Contact information:
Kees Vuik
Back to
home page
or
Afstudeer pagina
of Kees Vuik