Recreation
This page contains some recreational mathematics! Much of the material is written in Dutch.
Presentations and Workshops
Meetkunde die telt
Workshop bij Nationale Wiskunde Dagen 2012 binnen het thema Meetkundige Basisbegrippen van Michel Roelens. Zie onderaan voor wat materiaal.
Sommige stellingen in de wiskunde zijn zo fantastisch simpel en elegant, dat je je afvraagt: “Waarom ben IK daar niet op gekomen!” Deze voordracht gaat over precies zo’n stelling uit de meetkunde: eenvoudig maar verrassend.
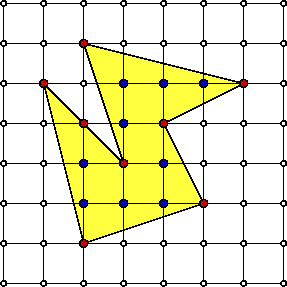
De hoofdrol wordt gespeeld door roosterveelhoeken, zoals die in de figuur. De hoekpunten zijn roosterpunten die als piketpaaltjes een gebied insluiten. De vraag is nu: hoe bepaal je snel de oppervlakte van dat gebied? Het elegante antwoord is, dat dit kan door roosterpunten te tellen!
We zullen deze stelling, het 'tweelingbroertje’ van Euler's veelvlakkenformule, op een elementaire manier bewijzen door middel van knippen en plakken. Dit is ook voor leerlingen goed te doen. Zo meten we oppervlaktes door te tellen. Maar, we zullen de stelling ook op z’n kop zetten: we tellen magische vierkanten door te meten.
We besluiten met een avontuurlijke stap in een nieuwe dimensie: het meten van volumes van ruimtelijke figuren. Zou dat ook kunnen door enkel te tellen?
- Een PDF van de presentatie
- Een klein werkblad met wat vragen en opdrachten
- Een oud artikel in Pythagoras over dit onderwerp
De wiskunde van het vouwen
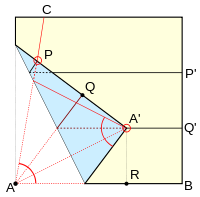
Voor de Leve de Wiskunde dag 2008, gaf ik een lezing over wiskunde en origami [PDF]].
Veel meer informatie over de wiskunde van het vouwen kun je vinden op de pagina van Robert Lang en Erik Demaine.
De wiskunde achter Good Will Hunting
In een voordracht (PDF) bij NWD 2007 over de film Good Will Hunting, kwamen de wiskundige problemen die Will in de film oploste aan de orde. Zie ook de volgende link.
Pythagoras

Het wiskundetijdschrift Pythagoras werd in 1961 opgericht door Bruno Ernst en richt zich voornamelijk op middelbare scholieren. Het verrast de lezer met leuke wetenswaardigheden, uitdagende puzzels en problemen en interessante wiskundige onderwerpen die de schoolwiskunde ver te buiten gaan.
Hieronder de stukjes die ik voor Pythagoras heb geschreven.
- Krulgetallen en een heel langzaam stijgende rij, januari 2016 [PDF].
- De Huwelijksstelling van Hall, januari 2009 [PDF].
- De stelling van Pick, september 2004 [PDF].
- Veelvlakken kleuren, februari 2003 [PDF].
- Het schaakbord van koning Shirham (deel 1 serie Grote Getallen), december 1999 [PDF].
- Hercules en Hydra (deel 2 serie Grote Getallen), februari 2000 [PDF].
- De tabel van Ackermann (deel 3 serie Grote Getallen), april 2000 [PDF].
- Onvoorstelbaar lange woorden (deel 4 serie Grote Getallen), juni 2000 [PDF].
- De driehoek van Pascal, april 2000 [PDF].
- Een piramide van Pascal, april 2000 [PDF].
- Het tellen van Sets, december 2000 [PDF].
Mathematical Olympiad
The first international mathematics olympiad (IMO) was held in Romania in 1959 with 7 participating countries from the former Soviet Bloc. In the last 50 years the IMO has grown to a spectacular annual competition with close to a hundred participating countries.
See the official IMO site for more information, and the IMO Compendium for the problems, training material and the scores of countries and individual participants.
A special event for the whole Dutch mathematics community was IMO2011 which was hosted in Amsterdam!
The Dutch mathematics olympiad (NWO) is a series of national mathematics competitions that brings the joy of solving interesting and unusual math problems to thousands of highschool students. In addition, it serves as a selection for the future members of the Dutch IMO team.
Other
This is a simple puzzle based on Chinese rings.




