Oefenopgaven
Contents
1.4. Oefenopgaven#
1.4.1. Rekenen met lijsten#
Opdracht: Voeg commentaar toe
Nog even oefenen met de stof van de vorige drie instructies.
Bestudeer het stukje code uit de paragraaf. Begrijp je wat daar gebeurd en waarom het zo is opgeschreven?
Voeg commentaar toe aan de code zodat dit duidelijk beschreven staat.
Hint
Met
lijst_var[i]vragen we heti-de element van de lijstlijst_varop.lijst_var.append(item)voegtitemtoe aanlijst_var.We slaan direct het resultaat van een berekening (bijv.
snelheid[i] * dt[i]) op in de lijst waarin ze terecht moet komen met.append().
1.4.2. NumPy#
Opdracht: Vergelijk de code
Bekijk de nieuwe code, waar we NumPy gebruikt hebben, en vergelijk deze met de code uit de vorige sectie. Kan je vinden welke regels met elkaar overeen komen?
Hint
Kijk eens in de documentatie van NumPy naar de werking van de functies np.diff en np.cumsum. Dit kan je, net als bij math, doen met
help(np.diff)
en
help(np.cumsum)
Opdracht: np.linspace
Lees de documentatie van np.linspace() door (help(np.linspace)) en beantwoord de volgende vragen:
Hoe kan je dit commando gebruiken om alle gehele getallen van 0 tot en met 100 te genereren?
En hoe kan je dit gebruiken om alle veelvouden van 0.1 tussen -1 en 2 te genereren?
1.4.3. Matplotlib#
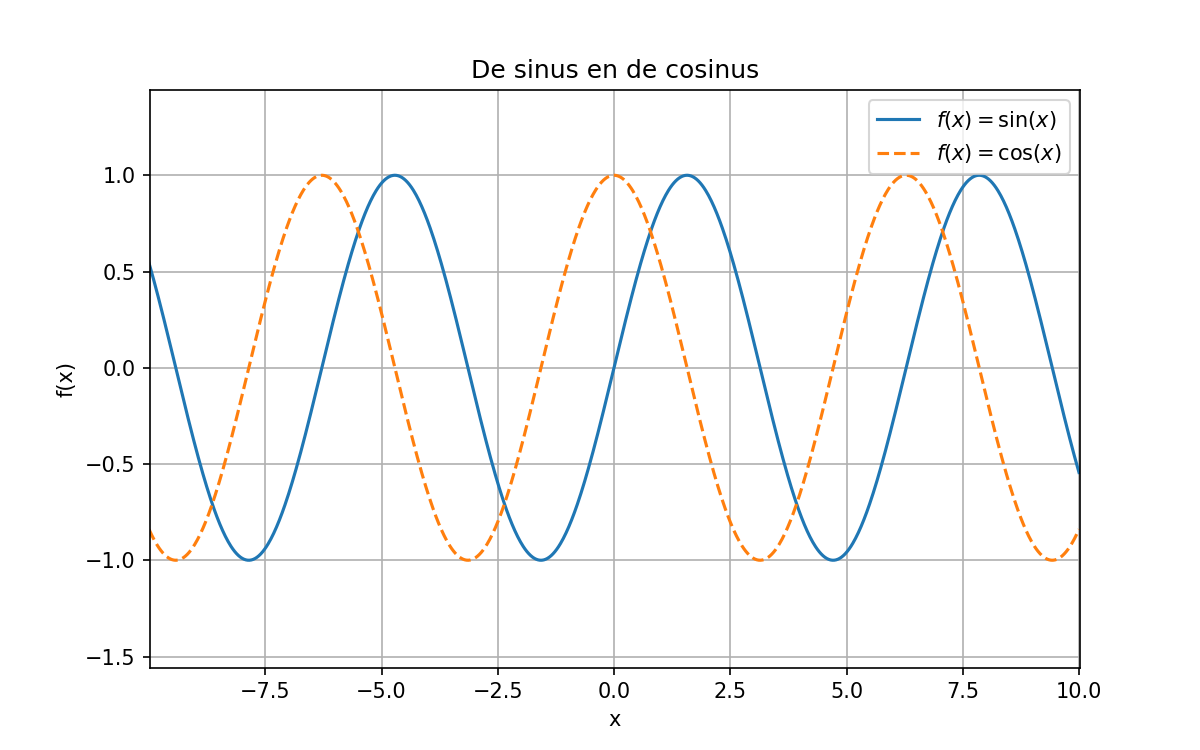
Opdracht: Pas de plot aan
Kopieer en plak deze code naar IDLE, en check of je hetzelfde resultaat krijgt.
Pas dan de code aan zodat:
De y-waarden
y1_valueseny2_valuesrespectievelijk de sinus en cosinus vanxaannemen (np.sin(x),np.cos(x)).De y-grenzen van de plot geschikte waarden krijgen (test evt. eerst wat je ziet als je alleen de y-waarden aanpast)
De labels die in de legenda komen de juiste informatie geven (gebruik liefst
\sin(x)en\cos(x), test evt. wat er verandert met of zonder de\)Pas de titel van de figuur aan.
Het resultaat zou er ongeveer zo uit moeten zien.
1.4.4. Afsluitende opdracht#
In deze periode sluiten wij elke week af met een opdracht waarin alles wat we tot dan toe geleerd hebben samen komt. Hiermee kan je kijken of je alles goed begrepen hebt en, misschien nog wel belangrijker, of je dit ook toe kan passen in je zelf geschreven code.
Je kan je antwoorden op deze vragen controleren in Vocareum. Kijk hiervoor op Brightspace.
Opdracht: Havenkraan 1
Deze vraag is aangepast van de basistoets Statica uit 2020
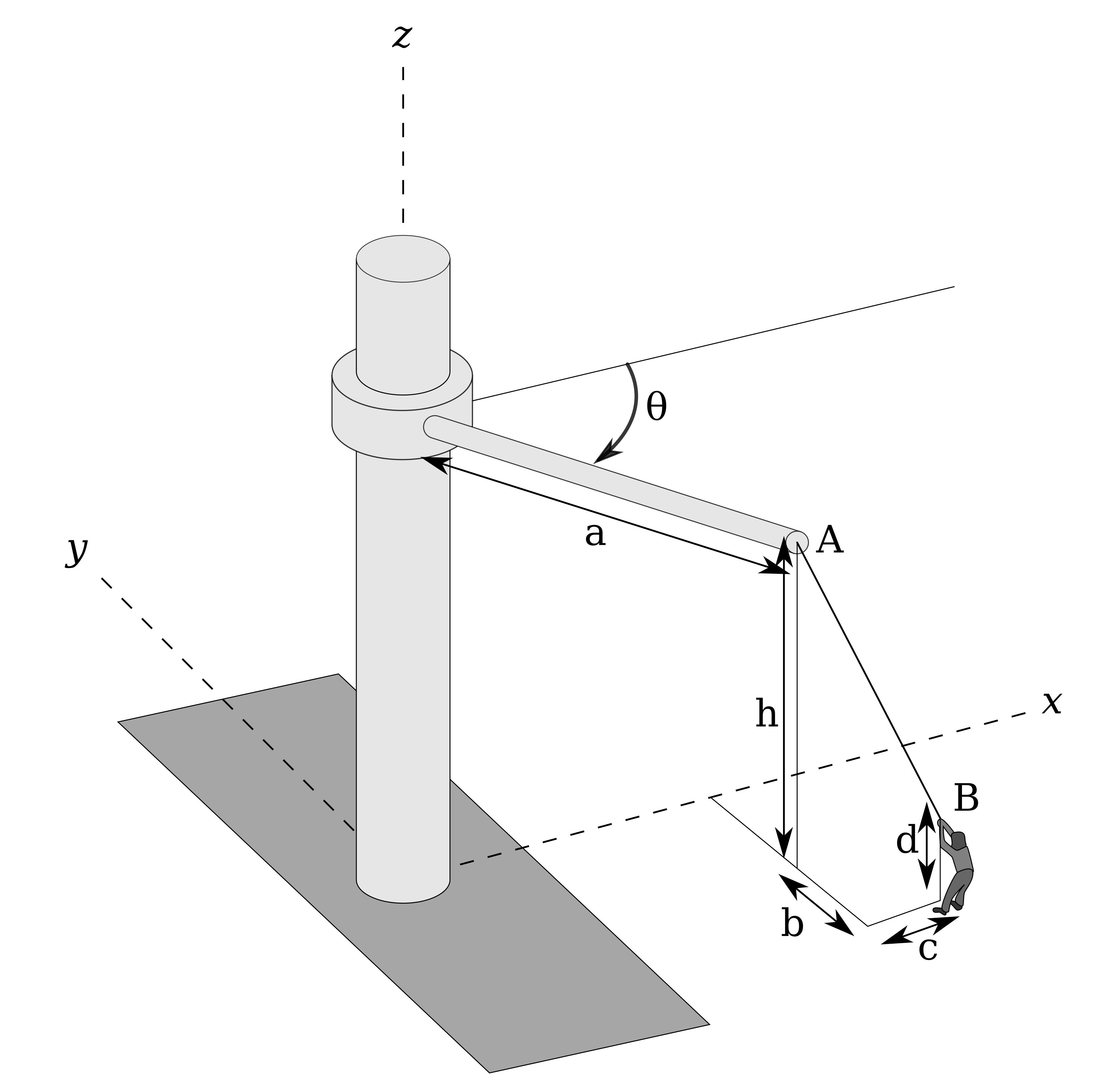
Een havenwerker probeert een havenkraan te draaien door aan de kabel \(AB\) te trekken met een kracht \(\mathbf{F}\) met een grootte van \(450\,\text{N}\). Hierdoor draait de kraan om de \(z\)-as, de resulteren hoek is aangegeven met \(\theta\).
De afmetingen in de kraan zijn gegeven in de figuur. Gebruik in deze opgave de volgende waarden:
Schrijf een script waarin je de kracht die de havenwerker op de kraan uitoefent bepaalt als een vector. Neem hierbij aan dat de afmetingen \(b, c, d\) en \(h\) gelijk blijven, ook wanneer de kraan draait.
Voer hiervoor de volgende stappen uit:
Sla de afmetingen \(a, b, c, d\) en \(h\) op als variabelen
Maak een numpy array aan met daarin de vector \(\mathbf{AB}\), die van \(A\) naar \(B\) wijst. Noem dit array
vec_AB.Deel dit array door zijn lengte om de eenheidsvector te krijgen (je kunt hiervoor
np.linalg.normgebruiken). Noem het resulterende arrayu_AB.Vermenigvuldig de eenheidsvector met de grootte van de kracht om de kracht als vector te krijgen. Noem het resulterende array
vec_F.
Opdracht: Havenkraan 2
We rekenen verder met dezelfde situatie als in de eerste opgave.
Om de havenkraan te draaien moet de werker een moment om de \(z\)-as uitvoeren. Dit moment zal variëren wanneer de havenkraan draait. Plot de \(z\)-component van het uitgeoefende moment als functie van de hoek \(\theta\). Ga er hierbij van uit dat zowel de grootte als de richting waarmee de werker aan de kabel trekt niet veranderen wanneer de kraan draait.
Voer hiervoor de volgende stappen uit:
Maak een array aan met alle hoeken \(\theta\) van \(0\) tot \(\frac{\pi}{2}\) in \(101\) stappen. Noem dit array
theta.Schrijf een functie
M(th), die voor de hoekthhet moment in de oorsprong berekent als gevolg van de kracht die de werker op de kraan uitoefentWe vinden het nuttige deel van het moment door alleen de \(z\)-component van de eerder berekende momentvector te nemen. Bereken dit voor elke hoek uit theta en sla het resultaat op als een array met de naam
vec_MzMaak een figuur waarin je het nuttige deel van het moment plot als functie van de hoek \(\theta\). Noem deze figuur
figen het assenstelsel waarin je plotaxLabel de assen van de figuur en voeg een beschrijvende titel toe.
