3.2. Numeriek Integreren

Op een vergelijkbare manier als het differentiëren kunnen we ook integreren op een discrete getallenlijn. Hiervoor maken wij gebruik van een Riemann-som.

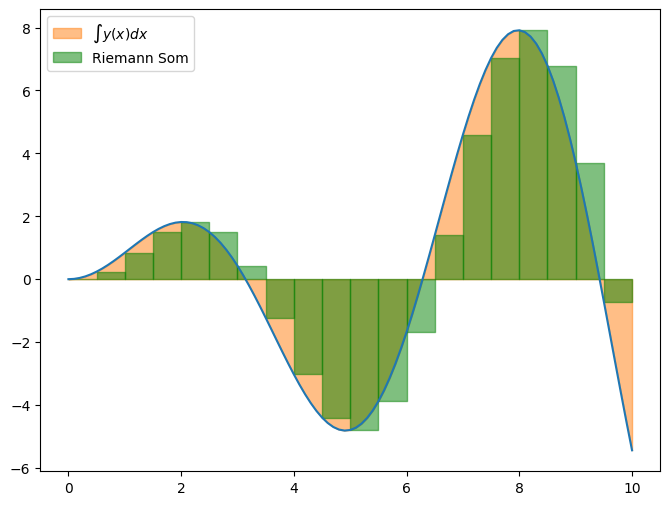
Zoals je weet bereken je met de integraal \(\int\limits_{x_1}^{x_2} y(x) \text{d}x\) het oppervlak onder de grafiek van \(y(x)\) tussen de punten \(x_1\) en \(x_2\). Wanneer we discrete datapunten hebben kunnen we dit oppervlak benaderen door een serie van rechthoeken. Het onderstaande stukje code illustreert hoe dit werkt.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
from matplotlib.collections import PatchCollection

def y(x):
    return x * np.sin(x)

x_values = np.linspace(0, 10, 101)
x_sample = np.linspace(0, 10, 21)

riemann_rectangles = []
riemann_oppervlaktes = []
for i in range(len(x_sample) - 1):
    w = x_sample[i + 1] - x_sample[i]
    h = y(x_sample[i])
    xy = (x_sample[i], 0)
    riemann_oppervlaktes.append(h * w)
    riemann_rectangles.append(Rectangle(xy, w, h,
                                        facecolor='green',
                                        alpha=.5,
                                        edgecolor='green'))

riemann_collection = PatchCollection(riemann_rectangles,
                                     facecolor='green',
                                     alpha=.5,
                                     edgecolor='green')

fig, ax = plt.subplots(1, 1, figsize=(8, 6))
ax.plot(x_values, y(x_values))
int = ax.fill_between(x_values, y(x_values), color='C1', alpha=.5)
som = ax.add_collection(riemann_collection)
ax.legend([int, riemann_rectangles[0]],
          [r'$\int y(x) dx$', 'Riemann Som'])
plt.show()

print(f'Riemann Som: {sum(riemann_oppervlaktes)}')
print(f'Integraal: {np.sin(10) - 10 * np.cos(10)}')

Riemann Som: 9.01973080190521
Integraal: 7.846694179875154

Zoals je ziet, is de afwijking tussen de eigenlijke integraal en de Riemann Som behoorlijk voor dit lage aantal rechthoeken. Dit zal echter snel afnemen wanneer het aantal rechthoeken toeneemt.

In deze opdracht ga je verder met deze techniek aan de slag om te controleren of je het helemaal begrijpt.

3.2.1. Integreren met NumPy

Ook voor integreren heeft NumPy een hele handige functie: numpy.trapz. Deze gebruikt een nog iets accuratere methode waarbij trapezoiden gebruikt worden in plaats van rechthoeken. Het onderstaande voorbeeld laat zien hoe je deze functie kunt gebruiken.

import numpy as np

def y(x):
    return x * np.sin(x) 

def Y(x):
    return np.sin(x) - x * np.cos(x)

x_sample = np.linspace(0, 10, 11)
y_sample = y(x_sample)

np_integraal = np.trapz(y_sample, x_sample)
an_integraal = Y(10) - Y(0)

print(f'NumPy integraal: {np_integraal}')
print(f'Analytische integraal: {an_integraal}')

NumPy integraal: 7.087834495645438
Analytische integraal: 7.846694179875154

In deze opdracht onderzoek je deze manier van integreren verder.