Differentiaalvergelijkingen
3.3. Differentiaalvergelijkingen#
Nu we weten hoe differentiëren en integreren door middel van code uitgevoerd kan worden kunnen we dit toepassen in modellen van complexere systemen. Hierin kunnen we de berekeningen die we hebben leren maken combineren met experimentele data en de resultaten hiervan plotten.
Als voorbeeld hiervoor kijken we naar de beweging van een raket. Tijdens het opstijgen verandert de luchtweerstandskracht op deze raket onder invloed van de veranderende snelheid en luchtdichtheid. Dit probleem is, mede doordat we geen functie voor de luchtdichtheid hebben, moeilijk analytisch op te lossen. Met een scriptje kunnen we echter wel goed het verloop van de hoogte en de snelheid van de raket berekenen.
De gegevens over de luchtdichtheid halen we uit dit bestand. Dit csv bestand lezen we in met gebruik van pandas.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv('data/Altitude_Density_Temperature.csv',
sep=';', skiprows=6)
print(df.head())
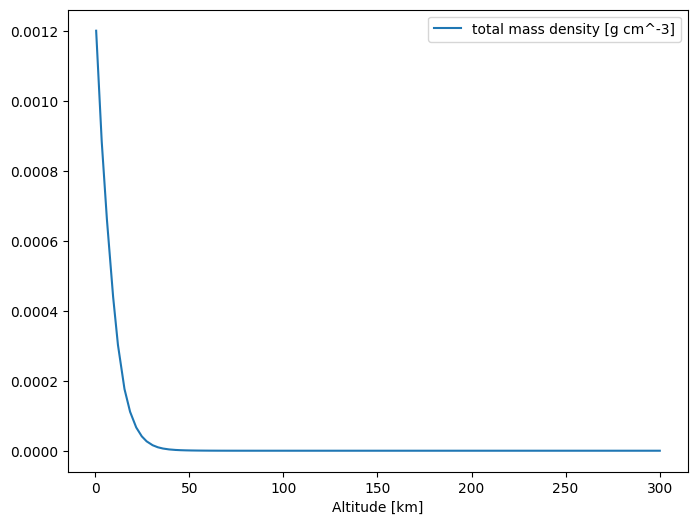
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
df.plot('Altitude [km]', 'total mass density [g cm^-3]', ax=ax)
plt.show()
Altitude [km] He number density [cm^-3] O number density [cm^-3] \
0 0.496198 1.310647e+14 0.0
1 3.455517 9.649064e+13 0.0
2 6.216816 7.214649e+13 0.0
3 9.513515 4.801398e+13 0.0
4 12.082837 3.300244e+13 0.0
N2 number density [cm^-3] O2 number density [cm^-3] \
0 1.953065e+19 5.239487e+18
1 1.437858e+19 3.857342e+18
2 1.075093e+19 2.884152e+18
3 7.154818e+18 1.919423e+18
4 4.917869e+18 1.319317e+18
AR number density [cm^-3] total mass density [g cm^-3] \
0 2.336159e+17 0.001202
1 1.719894e+17 0.000885
2 1.285973e+17 0.000661
3 8.558235e+16 0.000440
4 5.882509e+16 0.000303
H number density [cm^-3] N number density [cm^-3] \
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
Anomalous oxygen number density [cm^-3] Exospheric temperature [K] \
0 0.0 1027.318465
1 0.0 1027.318465
2 0.0 1027.318465
3 0.0 1027.318465
4 0.0 1027.318465
Temperature at `alt` [K]
0 279.605660
1 261.818491
2 240.563687
3 221.829985
4 216.205437
De luchtweerstandskracht wordt gegeven door
Waar \(\rho\) de luchtdichtheid is, \(A\) het frontaal oppervlak, \(C_w\) de luchtweerstandscoëfficient en \(v\) de snelheid. We nemen aan dat de raket een constante kracht \(F_{stuw}\) levert en een massa \(m\) heeft. We gebruiken de volgende gegevens:
We kunnen het gedrag van dit systeem berekenen als volgt:
Dit is in de onderstaande code gedaan door middel van de zogenaamde ‘Forward Euler’ methode. We maken daar gebruik van een volgende benadering. Let op dat we in de code met een index werken, in plaats van dat we een tijdsstip gebruiken om de snelheid/verplaatsing op een specifiek moment aan te duiden.
''' Gegevens van de Raket '''
massa = 5e2 # kg
Cw = 0.04
A = 3.16 # m^2
Fmotor = 5e3 # N
g = 9.81 # zwaartekrachtsversnelling (m/s^2)
def Fw(A, C_w, v, h):
''' Wrijvingskracht
Inputs: A Oppervlak in m^2
C_w Luchtweerstandscoefficient (eenheidsloos)
v snelheid in meter per seconde
h hoogte van de raket in meter
Outputs:
Luchtweerstandskracht in Newton
'''
# We gebruiken np.interp om de gegevens uit de csv te interpoleren
rho = np.interp(h, # de huidige hoogte in meter
1e3 * df['Altitude [km]'], # omgerekend naar meter
1e3 * df['total mass density [g cm^-3]']) # omgerekend naar kg/m^3
return -np.sign(v) * (1 / 2) * rho * A * C_w * (v ** 2)
def F_z():
''' Zwaartekracht op de raket
Inputs: -
Outputs: Zwaartekracht op de raket in N
'''
return -massa * g
def F_res(v, h):
''' Resulterende kracht op de raket
Inputs: v Snelheid in meter per seconde
h Hoogte in meter
Outputs:
Resulterende kracht op de raket in Newton
'''
return Fmotor + Fw(A, Cw, v, h) + F_z()
def versnelling(v, h):
''' Versnelling van de raket
Inputs: v Snelheid in meter per seconde
h Hoogte in meter
Outputs:
Versnelling van de raket in m/s^2
'''
return F_res(v, h) / massa
''' We stellen wat variabelen in voor de tijdstappen van de simulatie '''
t0 = 0
t1 = 1000
dt = 1 # s
tijd = np.arange(0, 1000, dt)
''' We maken twee arrays met nullen aan om de resultaten in op te slaan '''
hoogte = np.zeros(len(tijd))
snelheid = np.zeros(len(tijd))
''' In deze for-loop voeren we de berekeningen uit '''
for i, t in enumerate(tijd[:-1]):
snelheid[i + 1] = snelheid[i] + versnelling(snelheid[i], hoogte[i]) * dt
hoogte[i + 1] = hoogte[i] + snelheid[i] * dt
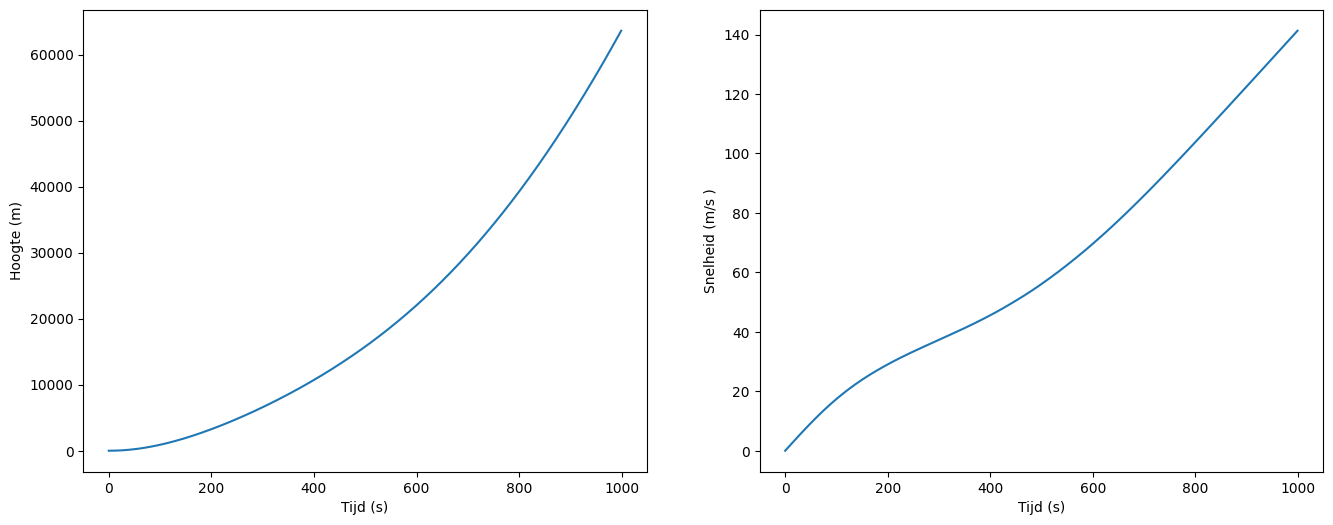
''' Ten slotte plotten we de resultaten '''
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
ax[0].plot(tijd, hoogte)
ax[0].set_xlabel('Tijd (s)')
ax[0].set_ylabel('Hoogte (m)')
ax[1].plot(tijd, snelheid)
ax[1].set_xlabel('Tijd (s)')
ax[1].set_ylabel('Snelheid (m/s )')
plt.show()