3.1. Numeriek Differentiëren

Een van de belangrijkste redenen waarom we leren programmeren is dat we daarmee gemakkelijk wiskundige problemen op kunnen lossen en zo een model van de werkelijkheid kunnen vormen. Dit helpt bij het ontwikkelen van een gevoel voor de systemen die we bestuderen en ook bij het iteratief optimaliseren van een ontwerp.

Echter, hier komen we nog wel een probleem tegen: In de wiskunde gaan we vaak uit van een continue reeks getallen waarop onze functies werken. In de computer is dit niet mogelijk. Altijd wanneer je een reeks getallen in de computer maakt zal er een bepaalde stapgrootte of resolutie zijn. Dat zagen we bijvoorbeeld al bij np.linspace(), waar we als derde argument opgaven uit hoeveel getallen de reeks moest bestaan. We kunnen dit aantal getallen natuurlijk wel groter maken, maar omdat alle getallen in het geheugen van de computer opgeslagen moeten worden is er een limiet aan hoe groot dit kan worden.

Gegeven dat we een eindig aantal punten hebben, hoe kunnen we dan alsnog een afgeleide of een integraal nemen? Daar zullen we het in deze instructie over hebben.

3.1.1. Differentiëren

Bij Analyse hebben we geleerd dat een afgeleide een limiet is:

\[ \frac{d y}{d x} = \lim_{h\to 0}\frac{y(x + h) - y(x)}{h} \]

Door deze limiet te nemen krijgen wij een functie van \(x\) die op elk punt van het bereik de helling (slope) van de grafiek weergeeft. Dit kunnen wij bijvoorbeeld gebruiken door vanuit een positie een snelheid te bepalen (\(v = \frac{d x}{d t}\)).

Wanneer wij dit op de computer doen bestaat deze limiet niet meer omdat \(h\) altijd een eindig getal zal zijn. Wij kunnen dus alleen de afgeleide die hier gegeven is benaderen. Daarvoor gebruiken we een kleine, maar eindige \(h\), die gegeven is door de afstand tussen de beschikbare datapunten.

In het voorbeeld hieronder zie je hoe dat eruit kan zien in Python code.

import numpy as np
import matplotlib.pyplot as plt

def afgeleide(x, y):
    ''' Bereken de nummerieke afgeleide van een functie
    
    inputs:
    -  x (list / numpy.array) - de x-waarden waarop de functie bemonsterd is.
    -  y (list / numpy.array) - de bijbehorende functie-waarden (moet dezelfde lengte als x hebben!).
    
    outputs:
    -  dydx (numpy.array) - de lengte van de schuine zijde
    '''

    # Maak een lege lijst aan voor het resultaat
    dydx = []

    # For-loop, van 0 tot len(x) - 1 
    # (omdat we x[i+1] en y[i+1] nodig hebben)
    for i in range(len(x) - 1):
        h = x[i + 1] - x[i]
        y0 = y[i]
        y1 = y[i + 1]
        dydx.append( (y1 - y0) / (h) )

    # Converteer het resultaat naar een numpy array
    dydx = np.array(dydx)

    return dydx

# Creëer data
x_waarden = np.linspace(-2, 2, 101)
y_waarden = 0.1 * x_waarden ** 3 - x_waarden ** 2 + 4 * x_waarden - 3

# Gebruik nummerieke afgeleide-functie
y_accent = afgeleide(x_waarden, y_waarden)

# Plot het resultaat
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
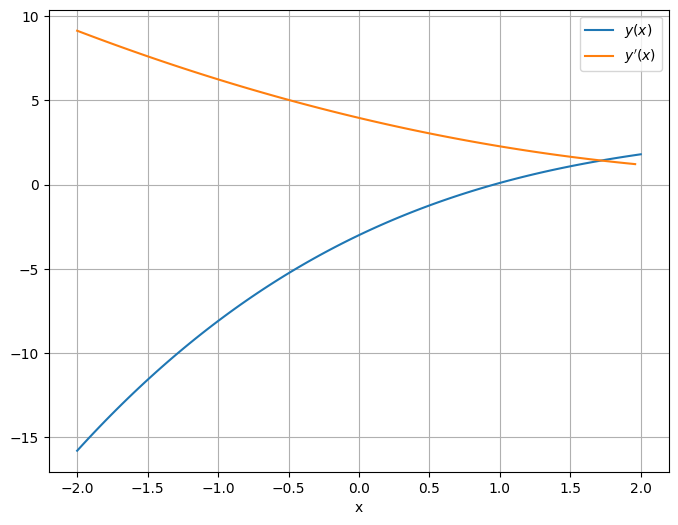
ax.plot(x_waarden, y_waarden, label='$y(x)$')
ax.plot(x_waarden[:-1], y_accent, label="$y'(x)$")

ax.legend()
ax.grid()
ax.set_xlabel('x')

plt.show()

Begrijp je goed wat deze code doet? Kijk eens naar deze opdracht om dit te controleren.

3.1.2. Differentiëren met NumPy

In het voorbeeld hierboven hebben we zelf een functie voor de afgeleide geschreven. Hierbij gebruikten we een for-loop om de hele lijst door te lopen en op elk punt een afgeleide te bepalen. Met NumPy kunnen we dit een stuk sneller en korter doen door de functie numpy.gradient() te gebruiken:

import matplotlib.pyplot as plt
import numpy as np

x_waarden = np.linspace(-2, 2, 101)
y_waarden = 0.1 * x_waarden ** 3 - x_waarden ** 2 + 4 * x_waarden - 3
dydx = np.gradient(y_waarden, x_waarden)

fig, ax = plt.subplots(1, 1, figsize=(8, 6))
ax.plot(x_waarden, y_waarden, label=r'$y(x)$')
ax.plot(x_waarden, dydx, label=r"$y'(x)$")

ax.grid()
ax.legend()
ax.set_xlabel('x')

plt.show()

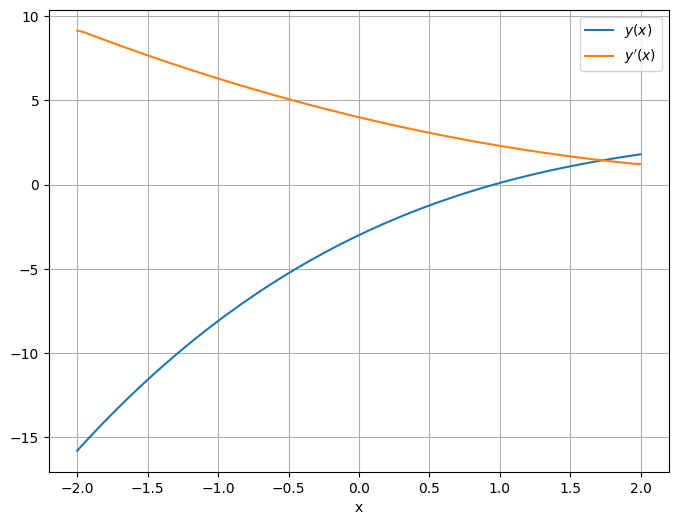
In de documentatie van numpy.gradient zie je dat hier een iets nauwkeurigere variant van de numerieke afgeleide wordt gebruikt: ‘central differences’ in plaats van ‘forward differences’. Dit zorgt er ook voor dat het array wat er als resultaat uit komt dezelfde lengte heeft als het array waarvan je de afgeleide neemt.

Ook over deze methode hebben we een opdracht geschreven waarmee je kan controleren of je begrijpt wat deze code doet.